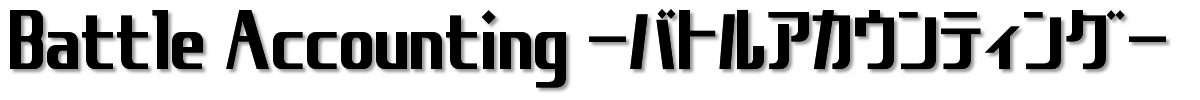Contents
未公開(未上場)企業のストック・オプション会計処理と本源的価値のポイント
今回は、未公開企業のストック・オプションについて理解を深めていきます。
この未公開企業の話は、要するに簡便法です。簡便法を使ってよいと言っています。
具体的な基準の文言は、以下の通りです。
未公開企業における取扱い
13. 未公開企業については、ストック・オプションの公正な評価単価に代え、ストック・オプションの単位当たりの本源的価値の見積りに基づいて会計処理を行うことができる。この場合、本会計基準の他の項で「公正な評価単価」を、「単位当たりの本源的価値」と読み替えてこれを適用する。この結果、特に第6項⑴の適用に関しては、付与日現在でストック・オプションの単位当たりの本源的価値を見積り、その後は見直さないこととなる。
ここで、「単位当たりの本源的価値」とは、算定時点においてストック・オプションが権利行使されると仮定した場合の単位当たりの価値であり、当該時点におけるストック・オプションの原資産である自社の株式の評価額と行使価格との差額をいう。
この条文で書かれているのは、原則=ストック・オプションの公正な評価単価だが、例外として未公開企業については、ストック・オプションの単位当たりの本源的価値の見積りに基づいて会計処理を行うことができるということですね。
この違いを理解するためには、原則法である公正な評価単価の計算方法と、本源的価値の意味について理解する必要がありますので、この場で深堀りして解説します。
なお、日本基準の適用を前提とします。
公正な評価単価の計算
公正な評価単価の算定方法⇒ブラック・ショールズ等
公正な評価単価の算定方法については、SO会計基準に、以下のように定められています。
SO会計基準
6. ストック・オプションの公正な評価単価の算定は、次のように行う。
(2) ストック・オプションは、通常、市場価格を観察することができないため、株式オプションの合理的な価額の見積りに広く受け入れられている算定技法を利用することとなる。算定技法の利用にあたっては、付与するストック・オプションの特性や条件等を適切に反映するよう必要に応じて調整を加える。ただし、失効の見込みについてはストック・オプション数に反映させるため、公正な評価単価の算定上は考慮しない。
では、「広く受け入れられている算定技法」とは何かですが、同48項にて、以下のような説明があります。
ストック・オプションに関しては、通常、市場価格が観察できないため、株式オプションの合理的な価格算定のために広く受け入れられている、株式オプション価格算定モデル等の算定技法を利用して公正な評価単価を見積ることとした。
「株式オプション価格算定モデル」とは、ストック・オプションの市場取引において、一定の能力を有する独立第三者間で自発的に形成されると考えられる合理的な価格を見積るためのモデルであり、市場関係者の間で広く受け入れられているものをいい、例えば、ブラック・ショールズ式や二項モデル等が考えられる。
つまり、ブラック・ショールズ式等の評価技法が、ここで求められている方法になります。
では、ブラック・ショールズ等の評価技法では、どのような計算が行われているのでしょうか?
ブラック・ショールズのイメージと計算内容
イメージ
このイメージを示したのが、以下です。
※こちらは、「「時価の算定に関する会計基準(案)」等の公表」というASBJからの資料に添付されていたものです。
こちらの図はイメージに過ぎませんが、まさにこの真ん中にある「評価技法」が、「ブラック・ショールズ」であると理解できますね。
今回の目的は全体像の理解にあるので、式の中身の解説は割愛させていただきますが、ここでの”アウトプット”は、概念的には、「将来権利行使時点のオプション利得の期待値の割引現在価値」になります。こちらを付与日の公正単価として算定しようとしています。
となれば、この公式にあてはめる”インプット”が気になりますね。
以下では、このインプットについて確認していきます。
ブラックショールズのインプット
ブラックショールズを前提とした場合のインプットは、実は適用指針6項に記載の、以下の項目になります。
| input | 別名 | 取得難度(レベル) | inputとoutputの相関関係(正=input↑⇒output↑) |
|---|---|---|---|
| (1) オプションの行使価格 | Strike | 1 | 負 |
| (2) オプションの満期までの期間(付与日から最終の権利行使期日まで) | Expiry | 1 | 場合による |
| (3) 算定時点における株価(算定時点は付与日又は条件変更日) | Spot Price | 1~2 | 正 |
| (4) 株価変動性 | Volatility | 3 | 正 |
| (5) ⑵の期間における配当額 | Dividend rate | 1~2 | 負 |
| (6) 無リスクの利子率(割引率) | Risk Free Rate | 1 | 正 |
これらのINPUTの取得難易度について、解説しておきます。
一般的に、(1)と(2)は所与の条件になり、計算時には通常既に与えられているものになるかと思います(なお、(2)の期間については税制適格要件との関連で、付与日から2年~10年の間とすることが多いです。)。
また、(3)(5)については対象会社が上場会社であればすぐに取得可能ですし、(6)は国債利子率等を参照すれば通常簡単に取得できます。
問題は、残った(4)の株価変動性すなわちボラティリティです。実は、inputの中ではこちらが公正な評価単価の計算にあたって最も重要で、かつ見積りの要素があるところになります。ここでのボラティリティは、株価の予想変動率を意味しますが、将来の株価の動きになりますので、予測をする必要があります。
SOを保有している人が、将来、権利行使できる株価を予測するイメージですね。
ボラティリティ(株価変動性)
このボラティリティ(株価変動性)には、実は2つあります。
1つは、ヒストリカル・ボラティリティ(過去の株価実績に基づく予測)です。
もう一つが、インプライド・ボラティリティ(当該企業の株式オプションが組み込まれた金融商品を含む株式オプションが市場で取引されている場合における、その市場価格から逆算される株価変動性)です。
それぞれの留意点が、適用指針10項にと11項に記載されていますが、ここではざっくり意味を掴みましょう。
ヒストリカル・ボラティリティは、その名の通り、過去の株価の変動実績を観察し、それをもとに将来の株価変動について見積る方法です。過去の情報自体、比較的観測しやすいメリットがあります。その一方で、株価情報を収集する対象期間が十分で適切であるかどうか、収集した株価の中に異常な情報が含まれていないかどうかなどの点で、注意が必要です。またそもそも、非上場会社のボラティリティを算定する場合は、類似企業(その会社ではない別会社)の株価情報などを参照せざるを得ない可能性があるため、非常に主観的な見積りになる可能性があります。
じゃあインプライド・ボラティリティを使おうと言いたいところですが、通常、自社の株式オプションが市場で活発に取引されていることは稀でしょう。また仮に市場取引されていたとしても、適用指針11項の条件を満たすとは限りません。そのため、実際はインプライド・ボラティリティを使用できるのは稀なケースであると考えられます。
以上より、一般的には、ヒストリカル・ボラティリティの算定を目指すことになります。
ブラックショールズ以外の算定技法
さて上記でブラック・ショールズのinputについてご紹介しました。
ただ、実はブラック・ショールズは、プレーン(単純化された)なオプションを評価する場合に、市場で最も使用されているものです(プレーン・バニラ=仕組みが単純な制度に対して有効な算定技法と言われます)。
なので、より複雑な条件を組み込まなければならない場合、別の評価モデルを検討することになります。
それが、基準にも示されている2項モデルや、モンテカルロ・シミュレーションです。
例えば、モンテカルロによれば、将来の相場を、与えられた確率変動条件(ボラテイリテイなど)のもと、何度もシミュレーション(試行)することになるので、複雑な株式市場条件(例:株価●●円の場合に権利行使可能になるなど)が付されていても、評価に組み込めるようになると言われています。
このように、SOの設計に応じて、評価技法を選ぶことになりますが、SO会計基準における公正な評価単価の算定技法といえるためには、「確立された理論を基礎としており、実務で広く適用されていること」という要件がある(適用指針5項)ので、なんでもかんでもOKというわけではないです。
まとめ
以上のように、公正な評価単価を算定するためのブラック・ショールズは、一般に広く使用される算定モデルであるものの、一部のインプット(ボラティリティ)については算定がより難しいことがわかりました。
また、ブラック・ショールズ以外の算定技法を使用する場合は、所謂プレーン・バニラではない制度に対応しようとしている状況が想定されますので、一般的にはさらに算定が難しい状況が想定されます。
これらのことから、実務では、一般的に、公正な評価単価を算定するために外部の専門家を利用することが多いです。
本源的価値の意味
さて、上記で述べてきた公正な評価単価を使用する方法を原則とする一方で、未公開企業(非上場企業)にて例外的に認められている方法が、本源的価値を利用する方法でした。
あらためて、本源的価値の意味について触れます。
「単位当たりの本源的価値」とは、算定時点においてストック・オプションが権利行使されると仮定した場合の単位当たりの価値であり、当該時点におけるストック・オプションの原資産である自社の株式の評価額と行使価格との差額をいう。
これはつまり、まさに、SOの権利行使により、本来の価格よりディスカウントされた金額で株式を取得できたことによる、その利ザヤ部分のことですね。本源的とは、「おおもとの」という意味で解釈して問題ないと思います。つまり、SOの根本的な価値の部分を意味しており、これが権利行使による利得であると解されます。
(税制非適格SOにて、実際は現金を得ていないのにもかかわらず給与所得として課税されてしまう、あの利得の部分です。)
ということは、計算に必要なのは、以下のみです。
- 対象となっている自社株式の時価
- 権利行使価格
このうち、通常②は所与の数値です。ということは、①がわかれば計算できてしまうということになります。
上述したブラック・ショールズ等に比べれば、物凄くラクな計算ということになりますが、実はいくつか論点があります。
非上場会社の株式評価
まず、上場会社ではないので、株価を簡単に参照することはできません。この点、以下のような適用指針の注意書きがあります。
適用指針
60. (略)一般に、市場価格を参照できない場合の株式価値の評価方法として、純資産法、キャッシュ・フロー法、配当還元法、取引事例比準法等、実務上様々な方法が用いられているが、(略)どのような評価方法が最も適切であるかは、それぞれの企業の置かれた状況や、評価のための技法の発展状況等、様々な条件によって異なり得る(略)。しかし、ここで利用すべき評価方法は、例えば、当該株式を第三者に新規に発行する場合の価格を決定する際に用いられるような合理的な評価方法である必要があると考えられる。61. (略)企業価値の実態を最もよく表し得る株式価値の評価方法は、企業の発展段階に応じて異なり得る。したがって、株式価値の評価方法に関しては、その開示を条件に、それぞれの評価時点において、企業価値を最もよく表し得ると考えられる方法を採用すればよいと考えられる。
結局、どの方法が良いかは明示していないため、一般的に理論的とされる方法を使用することになると思われます。
DCF法、マルチプル法、修正純資産法などを検討することが考えられますが、自社の株式価値の評価方法は注記することになります(適用指針73項)。
例えば、以下は新規上場申請のための有価証券報告書(Ⅰの部)のとある事例です。自社株式の評価は、DCFで算定している旨が注記されていますね。

費用がゼロになってしまう
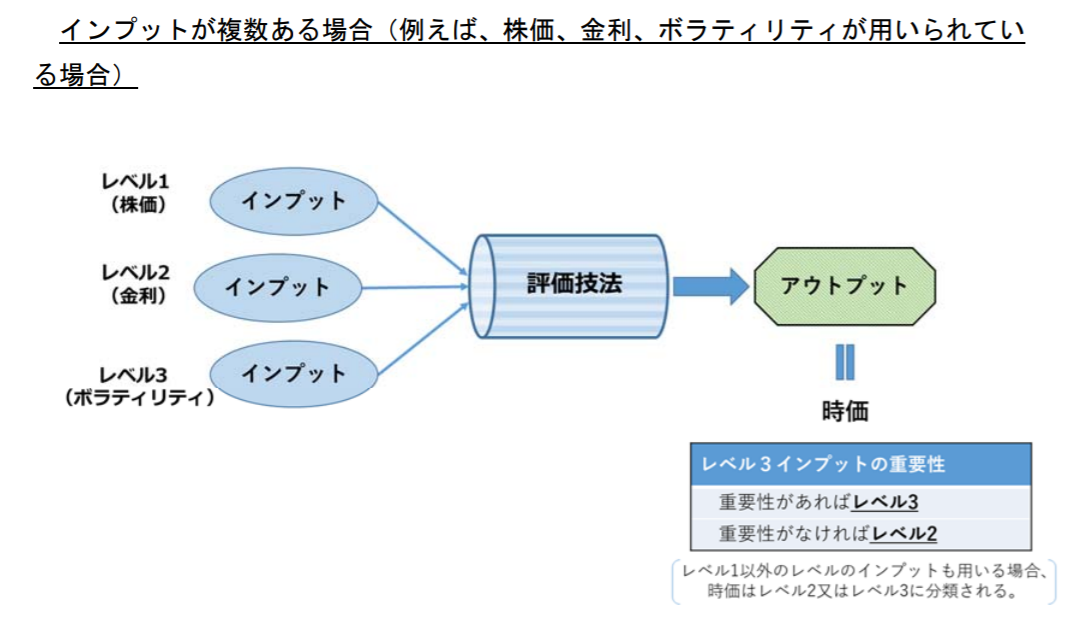
仮に、上記①の時価が、②を下回っていた場合、オプションの価値はゼロであるとされています。なぜなら、もし①<②の状況で権利行使をしたら、わざわざ権利行使してより価値の低いものを手に入れることになり行使者が損することになるため、合理的な行使者であれば、そのような権利行使は行わない(オプションを持っていない状態と同じ)と考えられるためです。
そして、未公開企業の段階では、①<②となっていることは稀ではありません。
そこで、会計基準もこの点を考慮し、権利行使日に至るまでその本源的価値を見直し、最終的に権利行使日において実現した価値に基づいて費用を計上する方法が検討されました。
しかし、この場合、本源的価値が株価によって変動する性質があることから、権利行使日までの株価の変動についても費用処理額に影響させることになってしまいます。もともとSOの費用は、従業員からのサービスを、オプション価格で間接的に測定しようとしたものですが、そのオプション価格が付与日後の株価変動がノイズとして入ってきてしまうため、付与日の公正価値で費用処理する本来の処理とも離れてしまいます。
そのため、本源的価値を見直して会計処理に反映することはせずに(付与日における本源的価値で会計処理し)、一方で注記を求めることになりました。
すなわち、ストック・オプションの各期末における本源的価値の合計額及び各会計期間中に権利行使されたストック・オプションの権利行使日における本源的価値の合計額につき、注記が必要になります(適用指針63項)。
なお、費用処理のロジックについては、こちらもご参照ください。
(参考)本源的価値と時間的価値
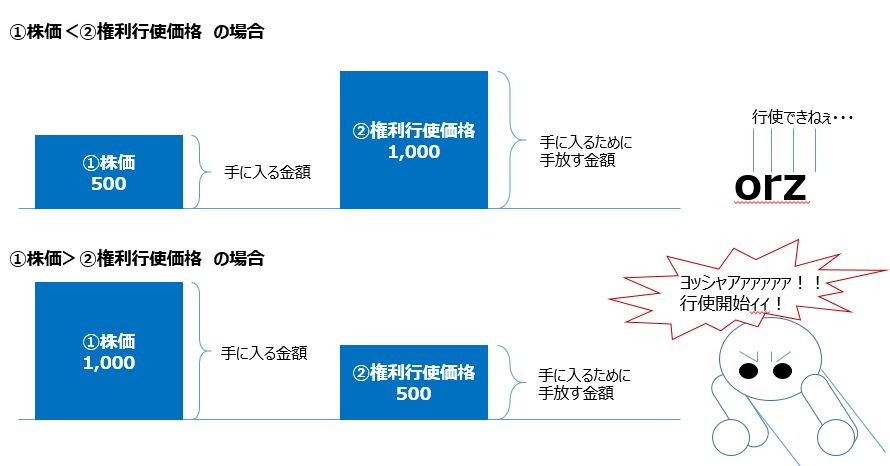
本源的価値というキーワードは、オプションを理解するうえでは欠かせないものです。しかし実際は、オプションの価値は本源的価値だけではありません。
つまり、オプションの価値=本源的価値+時間的価値として表現されます。SOを手に入れた人は、本源的価値と時間的価値を手に入れていることになります。
本源的価値とは、上述のとおりSOの行使によって直接得られる利得です。
そして時間的価値とは、「将来発生する可能性のある本源的価値」を意味します。つまり、たとえ現在の株価では権利行使できなくても、権利行使のための残存期間が十分に確保されている場合、株価が上がって有意な本源的価値を手に入れられるチャンスがあります。このチャンスの価値についても、SOの価値に含まれるという考え方です。
この時間価値の性格上、以下のことが言えます。
- 残存期間が長いほど、時間的価値は増加する
- 株価の予想変動率(ボラティリティ)が大きいほど、時間的価値は増加する
- 時間の経過とともに時間的価値は低くなり、オプションの満期日にはゼロとなる
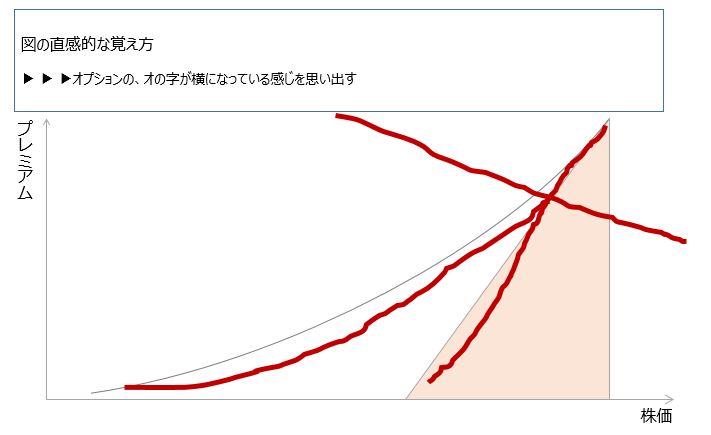
このような、SO(コール・オプション)に関するプレミアムの説明としてよく図示して示されるのが、以下です(出所:wikipediaなどをもとに筆者作成・加筆)。
アウト・オブ・ザ・マネーは、SO保有者が損をしてしまう状態で、イン・ザ・マネーはその逆の得をする状態です。オプションの説明で良く出てくる用語ですが、この図であわせて表現可能ですので覚えてしまいましょう。「アウト・オブ・眼中」と同じ感覚で覚えられますね。
なお、ストック・オプションの各期末における本源的価値の合計額につき注記が必要と述べましたが、当期末において、株価が権利行使価格以下にとどまる状況においては、本源的価値がゼロになるため、以下のような注記をすることになると考えられます。

ところで、この図自体の覚え方ですが、例えば以下のような方法はどうでしょうか。
オプションのオの字で覚える方法です。蛇足かもしれませんが、これなら速攻思い出せますね。
まとめ
いかがでしたでしょうか。
未公開(非上場)企業の処理について基準に書かれていますが、実は基本的なオプションの理解がないと、内容はよくわからないので、オプションの理解を含めて解説をしてきました。
これを機に、理解を深めていただければ幸いです。
なお、今回参考にした書籍は以下の通りです。
 |
【中古】 ストック・オプション会計と評価の実務 会計とオプション理論の架け橋を目指して / 中嶋 克久, 野口 真人 / 税務研究会出版局 [単行本]【メール便送料無料】【あす楽対応】 価格:30,314円 |
![]()
 |
株式報酬の会計実務 日本基準とIFRSの論点詳解 [ あずさ監査法人 ] 価格:5,940円 |
![]()